A Finite Trip with Kakeya
Following Kakeya’s needle to new mathematics
By Evelyn Lamb on May 31, 2018
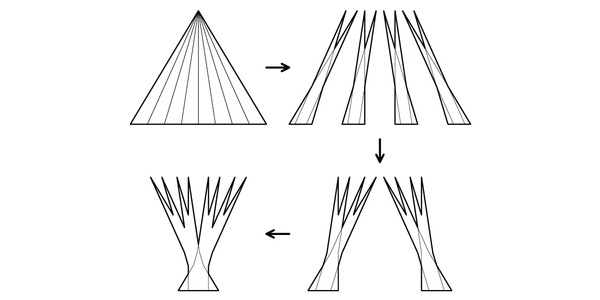
An illustration of a process that can create small Besicovitch sets. The triangle is cut up and reassembled into a set that contains unit-length segments pointing in every direction. Credit: Jazzam and Mikhail Ryazanov Wikimedia
Last year, I wrote about the Kakeya needle problem, a mathematical morsel I turn to for reassurance when I’m worried I might be stuck. The problem asks for the minimal area you need to turn a thin needle around in the plane. Below is one example of a needle turning around in a small area in a plane.
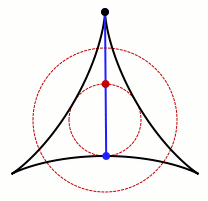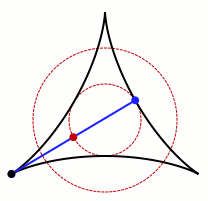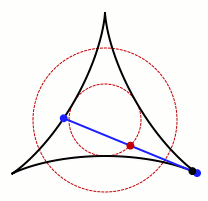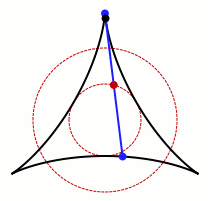
An animation of one set that allows Kakeya's
needle to turn around. Credit: Claudio Rocchini
Wikimedia (CC BY-SA 3.0)
Surprisingly, a needle can be turned around in a set with arbitrarily small area. This fact was proved by Abram Samoilovitch Besicovitch in 1928. He based the result on his prior work concerning sets in the plane that contain a unit-length segment pointing in every direction. These sets are called Besicovitch sets in his honor.
Besicovitch sets can look really cool, so I was excited when I saw a paper about minimal Besicovitch arrangements on the preprint server arxiv.org. When I started reading it, though, I was both disappointed and intrigued. The paper is not about Besicovitch sets in the plane, so I wasn’t going to see a bunch of pretty pictures, but I got to learn about a different version of the Kakeya needle problem. The paper looks at a translation of the Kakeya needle problem to a different mathematical setting, the world of finite fields and planes.
We’re used to doing arithmetic with infinite number fields like the real numbers, but we can also define the basic operations on finite sets of numbers. For example, in modular arithmetic, also called clock arithmetic, you have a modulus—say, 12—and when you add or multiply two numbers, you look at the remainder when you divide by the modulus. The system doesn’t seem as foreign when you think about the fact that five hours after 10:00 is 3:00. We’re used to doing arithmetic with a modulus of 12 or 24 when it comes to telling time. (For technical reasons, for the finite version of the Kakeya needle problem, the modulus needs to be a prime number or a power of a prime number. There are no Kakeya clocks!)
More:
https://blogs.scientificamerican.com/roots-of-unity/a-finite-trip-with-kakeya/

